The Princeton University Press has brought out the ninth volume of a series, since 2010, of selected writing that explores the range and oddities of math, as well as the connections of math with minds, life and society. For the most part, the collection, “Best writing on mathematics”, is accessible to persons without special training in math and informative for mathematicians as well. An instance in the collection is the piece on the chances of winning at a game of dice.

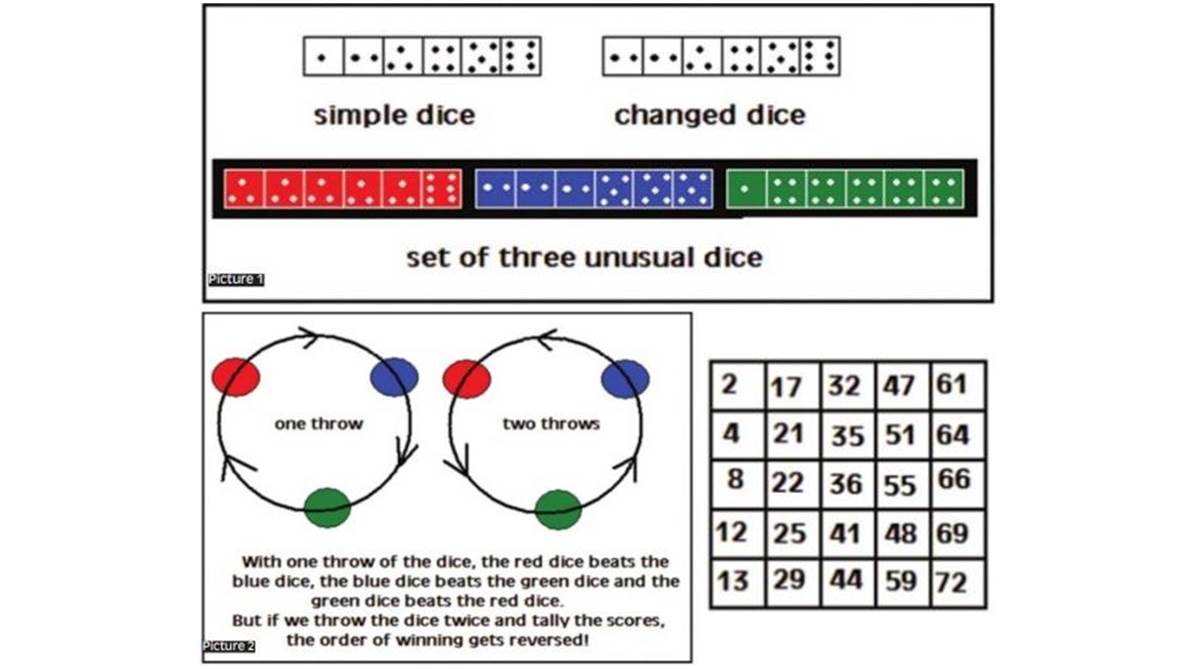
As we know, a dice has six sides, marked as shown in the first picture. And there is an equal chance that either of two players would roll a higher or lower number. But if one of the dice had altered faces, like in picture, which is with two sides marked as a throw of “2” and none of “1”. It is easy to see that this dice would win more often than the other one.

The author of the piece now proposes a set of three unusual dice, the third part of the picture. The red dice has five sides marked with “3” and one with “6”. The Blue has three sides marked with “2” and three sides with “5”. It is easily worked out that the red dice beats the blue dice seven times out of 12 throws. And similarly, if we consider the blue and green dice, we can work it out that the blue dice beats the green dice, which has five sides marked with “4” and one side with “1”, the same seven times out of 12.

Now comes the surprising part.

When we consider the red and the green dice, it is the green dice that beats the red dice, 25 times out of 36 throws, which is better than seven times out of 12! It turns out to be like a game of rock, paper and scissors! The three dice work in a circle like in the second picture.

And the marvel does not stop here, if the game is played with two throws of the dice in place of one throw, the order of scoring reverses, as shown in the picture.

The article then examines the case of playing with more than two players and more than three dice and the possibility of beating either or both players and successive cases of increasing complexity.

Another article in the book examines the popular club and party game of Bingo, also known as Housie or Tambola. The game is played with cards that have five columns and five rows. Each column has five numbers, randomly chosen, between 1 and 15 in the first column, between 16 and 30 in the second column and then 31 to 45, 46 to 60 and 61 to 75, like the instance shown in the third picture.

There can be many players, dozens, in fact and each has a card with different numbers, randomly chosen. The person conducting the game then draws numbers, from “1” to “75”, at random, from a box and calls them out. And players who find the numbers called out in their cards, score those numbers out. The winner is the one who first scores out all the numbers in any row or any column.

We can see that if we draw numbers at random and score out numbers in our own card, when the numbers are drawn, we are equally likely to first score out a whole row or a whole column. But the remarkable thing, the paradox, the article says, is that when a group is playing the game, the chance of the winner scoring out a row is twice that of completing a column!

In the analysis of the game, the author first looks at a case of row or a column getting scored out within the very first five draws. For this to happen, for a row, once the first number is called, the second number has to belong to a different column. The second number should hence be one of the 60 numbers belonging to other columns, out of the 74 numbers that are left. The chance of this happening is 60/74. Similarly, the chance of the third number belonging to one of the three remaining columns is 45/73. And then, for the fourth and fifth numbers, it is 30/72 and 15/71.

The product of these four probabilities is:

And it can be said that it is pretty unlikely.

In the same way, we can work out the chance for a vertical column as:

Scoring out a vertical column is thus 50 times less likely. This is when we think of the game being completed in the first five calls. From the probability, which is just over 0.04, this may happen only once in about 22 times the game is played. The author then works out what it would be like if the game carried on to the sixth call. Here, the calculation becomes complex, as there are different combinations, basically related to which of the first five calls did not result in scoring out a number in the winning combination. But the result is that the winning chances of both the rows and the columns increase, but the ratio falls – the row is now only about 23 times more likely to win than a column. And in this way, the chances of a row being filled before a column reduces, till the 13th call, when rows and columns are equally likely, and thereafter, if the game should go on, the columns become more likely. The game is most likely to be solved at the ninth call and the game must get solved within 17 calls!

The other articles in the book deal with contemporary issues, like scientific discovery by using information technology, whether brute force methods, which use computers’ muscle, can solve all kinds of problems, the question of how mathematics shows up in so many aspects of nature, how Babylon was ahead of the Greeks in Trigonometry and methods of math pedagogy. The first chapter of the book, which speaks about the motivation and the value of math, makes a point that the kind of people who do math may take us by surprise. And the happy idea that there is a mathematician lurking in most of us.

(The writer can be contacted at response@simplescience.in)